خوارزمية الترتيب بالدلاء

فكرة عمل خوارزمية الترتيب بالدلاء

بيانات عامّة

الصنف	خوارزمية ترتيب
بنية البيانات	مصفوفة

الأداء

أسوء حالة	${\displaystyle O\left(n^{2}\right)}$
الأداء الوسطي	${\displaystyle O\left(n+{\frac {n^{2}}{k}}+k\right)}$, حيث إن 𝑘 هو عدد الدلاء. ${\displaystyle O(n),{\text{when }}k\approx n}$.
أسوأ حالة تعقيد مكاني	${\displaystyle O(n+k)}$
أوسط حالة تعقيد مكاني	${\displaystyle O(n+{\frac {n^{2}}{k}}+k)}$

تعديل - تعديل مصدري - تعديل ويكي بيانات

الترتيب بطريقة الدلو أو الفرز بالدلاء (بالإنجليزية: Bucket sort)، أو الترتيب بالصناديق أو الفرز بالحاويات (بالإنجليزية: bin sort)، هو خوارزمية ترتيب تعمل عن طريق توزيع عناصر المصفوفة على عدد من الدلاء (الحاويات). بعد ذلك، يتم ترتيب محتويات كل دلو على حدة، إما باستخدام خوارزمية ترتيب مختلفة، أو بإعادة تطبيق نفس خوارزمية الترتيب بالدلاء بشكل متكرر على الدلو نفسه. تُعد هذه الخوارزمية أحد أنواع الترتيب بالتوزيع (بالإنجليزية: Distribution Sort)، وهي تعميم لطريقة "ترتيب برج الحمام" أو "ترتيب الخانات" (بالإنجليزية: Pigeonhole Sort) الذي يسمح بمفاتيح متعددة (قيم متعددة) في كل دلو، وهي قريبة في الأسلوب من الترتيب المنازلي أو "فرز الأسس" (بالإنجليزية: Radix Sort) خاصةً في أسلوب الترتيب من الرقم الأكثر أهمية إلى الأقل. يمكن تنفيذ الترتيب بطريقة الدلاء باستخدام المقارنات وبالتالي يمكن اعتبارها أيضًا خوارزمية ترتيب بالمقارنة (بالإنجليزية: Comparison Sort).

يعتمد مدى تعقيد التحليل الحسابي لهذه اخوارزمية على:

1. الخوارزمية المستخدمة لترتيب محتويات كل دلو،
2. وعدد الدلاء التي يجب استخدامها،
3. وما إذا كانت البيانات المُدخلة موزعة توزيعًا منتظمًا أم لا.

وتعمل خوارزمية الترتيب بطريقة الدلاء على النحو التالي:

1. أولا، إنشاء مجموعة من "الدلاء" الفارغة في البداية على شكل مصفوفة.
2. التوزيع (بالإنجليزية: Scatter): المرور على عناصر المصفوفة الأصلية، ووضع كل عنصر في دلوه المناسب.
3. ثم ترتيب كل دلو غير فارغ على حده.
4. التجميع (بالإنجليزية: Gather): المرور على الدلاء بالترتيب، وإعادة جميع العناصر مرة أخرى ووضعها في المصفوفة الأصلية.

function bucketSort(array, k) is
    buckets ← new array of k empty lists
    M ← 1 + the maximum key value in the array
    for i = 0 to length(array) do
        insert array[i] into buckets[floor(k × array[i] / M)]
    for i = 0 to k do 
        nextSort(buckets[i])
    return the concatenation of buckets[0], ...., buckets[k]

لنفترض أن اسم المصفوفة المطلوب ترتيبها هو "array"، وأن k هو عدد الدلاء التي سيتم استخدامها. من الممكن حساب أقصى قيمة مفتاحية في زمن خطي من خلال التكرار على جميع المفاتيح مرة واحدة. لابد من استخدام الدالة الأرضية لتحويل الأعداد العشرية إلى أعداد صحيحة، وربما يتطلب ذلك أيضًا تحويل نوع البيانات.

الدالة nextSort هي دالة ترتيب تُستخدم لترتيب كل دلو على حدة. تقليديا، من المعتاد استخدام الترتيب بالإدراج (بالإنجليزية: Insertion Sort)، ولكن يمكن استخدام خوارزميات أخرى كذلك، مثل خوارزمية الترتيب الانتقائي (بالإنجليزية: Selection Sort) أو خوارزمية الترتيب بالدمج (بالإنجليزية: Merge Sort).

يؤدي استخدام bucketSort (المبينة أعلاه داخل الصندوق الوصفي) كدالة nextSort، إلى إنشاء نوع قريب من خوارزمية الترتيب المنازلي (بالإنجليزية: Radix Sort)، وفي حالة ما إذا كانت n = 2 فإنها تُقابل في هذه الحالة الخاصة خوارزمية الترتيب السريع وإن كان ذلك قد يتم باختيار محاور (بالإنجليزية: pivots) غير جيدة.

بعض الخوارزميات قد يكون لديها أسوأ حالة نادرة الحدوث (بالإنجليزية: Worst-case analysis)، وعليه يتم دراسة أداء الخوارزمية في أسوأ حالة أي في السيناريو الأكثر سوءًا عندما تواجه الخوارزمية المدخلات التي تجعلها تعمل بأقصى وقت ممكن أو تستخدم أكبر قدر من الموارد مثل الذاكرة، والهدف من هذا التحليل هو فهم الحد الأعلى لأداء الخوارزمية، مما يساعد في ضمان أن الخوارزمية لن تتجاوز حدًا معينًا من الوقت أو المساحة حتى في الظروف الأكثر صعوبة.

ومن أجل الحصول على صورة أكثر اكتمالاً للخوارزمية هناك تحليل الحالات الغالبة (بالإنجليزية: Average-case analysis) كما يوجد تحليل أفضل حالة (بالإنجليزية: Best-case analysis).

وتكمن أهمية تحليل أسوأ حالة للخوارزمية في التالي:

• يساعد في ضمان موثوقية الخوارزمية حتى في الظروف غير المثالية.
• يُستخدم في المقارنة بين الخوارزميات لاختيار الأفضل لسيناريوهات حرجة.
• مفيد في التطبيقات التي تتطلب ضمانات زمنية صارمة، مثل لأنظمة الوقت الحقيقي (بالإنجليزية: Real-time systems).

عندما تحتوي المدخلات على عدة مفاتيح متقاربة من بعضها (تكتل)(بالإنجليزية: clustering)، فإن هذه العناصر يُحتمل أن تُوضَع في نفس الدلو، مما يؤدي إلى وجود بعض الدلاء التي تحتوي على عناصر أكثر من المتوسط.

تحدث أسوأ حالة عندما توضع جميع العناصر في دلو واحد فقط، وعندها، يصبح الأداء العام معتمدًا بالكامل على الخوارزمية المستخدمة لترتيب هذا الدلو، على سبيل المثال: ${\displaystyle O(n^{2})}$ عند استخدام الترتيب بالإدراج، أو ${\displaystyle O(n\log(n))}$ عند استخدام خوارزميات الترتيب بالمقارنة مثل خوارزمية الترتيب بالدمج.

في الحالة التي يتم فيها توزيع المدخلات بشكل موحد، يتم في الخطوة الأولى تجهيز الدلاء (بالإنجليزية: initialize) والعثور على الحد الأقصى لقيمة المفتاح في المصفوفة، خلال زمن قدره ${\displaystyle O(n)}$.

فإذا كان من الممكن إجراء القسمة والضرب في وقت ثابت، فإن توزيع (بالإنجليزية: Scattering) كل عنصر إلى دلوه يكلف أيضًا زمناً قدره ${\displaystyle O(n)}$، وهذه هي الخطوة الثانية.

لنفترض أنه سيتم استخدام الترتيب بالإدراج لترتيب عناصر كل دلو، فعندها تتكلف الخطوة الثالثة زمناً قدره ${\displaystyle O(\textstyle \sum _{i=1}^{k}\displaystyle n_{i}^{2})}$، حيث ${\displaystyle n_{i}}$ هي عدد العناصر في الدلو رقم ${\displaystyle i}$.

وبما أننا نريد حساب بالوقت المتوسط، فيجب تقييم التوقع الرياضي: ${\displaystyle E(n_{i}^{2})}$ بدلًا من القيمة الفعلية.

ولنفترض أن ${\displaystyle X_{ij}}$ هي المتغير العشوائي الذي يساوي ${\displaystyle 1}$ إذا تم وضع العنصر ${\displaystyle j}$ في الدلو ${\displaystyle i}$ ، أو يساوي ${\displaystyle 0}$ خلاف ذلك.

يصبح لدينا عدد العناصر في الدلو يساوي: ${\displaystyle n_{i}=\sum _{j=1}^{n}X_{ij}}$ .

ولذلك،

 ${\displaystyle {\begin{aligned}E(n_{i}^{2})&=E\left(\sum _{j=1}^{n}X_{ij}\sum _{l=1}^{n}X_{il}\right)\\&=E\left(\sum _{j=1}^{n}\sum _{l=1}^{n}X_{ij}X_{il}\right)\\&=E\left(\sum _{j=1}^{n}X_{ij}^{2}\right)+E\left(\sum _{1\leq j,l\leq n}\sum _{j\neq l}X_{ij}X_{il}\right)\end{aligned}}}$

السطر الأخير يفصل عملية الجمع إلى حالتين هما: الحالة ${\displaystyle j=l}$ والحالة ${\displaystyle j\neq l}$.

وبما أن احتمال توزيع أحد المدخلات إلى الدلو ${\displaystyle i}$ هو ${\displaystyle 1/k}$، فإن ${\displaystyle X_{ij}}$ سوف تساوي 1 باحتمالية ${\displaystyle 1/k}$، وفي غير ذلك سوف تساوي 0.

 ${\displaystyle E(X_{ij}^{2})=1^{2}\cdot \left({\frac {1}{k}}\right)+0^{2}\cdot \left(1-{\frac {1}{k}}\right)={\frac {1}{k}}}$
 ${\displaystyle E(X_{ij}X_{ik})=1\cdot \left({\frac {1}{k}}\right)\left({\frac {1}{k}}\right)={\frac {1}{k^{2}}}}$

وبإجراء عملية الجمع، سيكون لدينا

 ${\displaystyle E\left(\sum _{j=1}^{n}X_{ij}^{2}\right)+E\left(\sum _{1\leq j,k\leq n}\sum _{j\neq k}X_{ij}X_{ik}\right)=n\cdot {\frac {1}{k}}+n(n-1)\cdot {\frac {1}{k^{2}}}={\frac {n^{2}+nk-n}{k^{2}}}}$

وأخيرا، فإن "تعقيد العملية" سيكون:

${\displaystyle O\left(\sum _{i=1}^{k}E(n_{i}^{2})\right)=O\left(\sum _{i=1}^{k}{\frac {n^{2}+nk-n}{k^{2}}}\right)=O\left({\frac {n^{2}}{k}}+n\right)}$ .

الخطوة الأخيرة في خوارزمية الترتيب بالدلاء، وهي إعادة تجميع ودمج (بالإنجليزية: concatenating) جميع العناصر المُرتبة من كل دلو، تتطلب وقتاً قدره ${\displaystyle O(k)}$.

لذلك، فإن "إجمالي تعقيد العملية" سيكون ${\displaystyle O\left(n+{\frac {n^{2}}{k}}+k\right)}$.

لاحظ أنه إذا تم اختيار k بحيث تكون ${\displaystyle k=\Theta (n)}$ ، فإن خوارزمية الترتيب بالدلاء ستعمل في متوسط زمن مقداره ${\displaystyle O(n)}$، بشرط أن تكون المُدخلات موزعة توزيعًا منتظمًا.^[1]

إحدى التحسينات الشائعة هي إعادة العناصر غير المُرتبة من الدلاء إلى المصفوفة الأصلية أولاً، ثم تنفيذ الترتيب بالإدراج على المصفوفة بالكامل:

ونظراً لأن زمن تنفيذ الترتيب بالإدراج يعتمد على مدى ابتعاد كل عنصر عن موضعه النهائي، فإن عدد المقارنات يظل صغيرًا نسبيًا، ويتم استغلال التسلسل الهرمي للذاكرة بشكل أفضل عن طريق تخزين القائمة بشكل متجاور في الذاكرة.^[2]

إذا كان توزيع البيانات المُدخلة معروفًا أو يمكن تقديره، فغالبًا ما يمكن اختيار الدلاء بحيث تحتوي على كثافة ثابتة بدلاً من أن تكون ذات حجم ثابت فقط. وهذا يتيح تحقيق تعقيد زمني متوسط مقداره ${\displaystyle O(n)}$ حتى دون الحاجة إلى أن تكون البيانات موزعة توزيعًا منتظمًا.

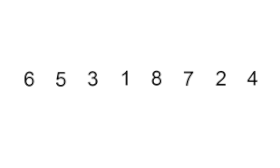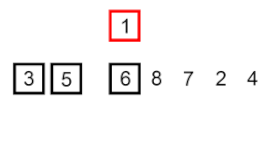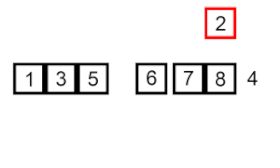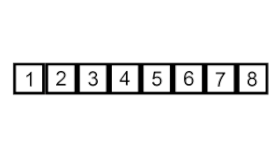
تعمل الصيغة المألوفة والأوسع استخدامًا لخوارزمية الترتيب بالدلاء، على قائمة مكونة من عدد n من المدخلات الرقمية قيمهم تتراوح بين الصفر وبعض القيم القصوى M، ويُقسَّم المجال العددي (بالإنجليزية: range) إلى عدد b من الأقسام المتساوية، حجم كل منها يساوي M / b.

إذا تم ترتيب كل دلو باستخدام خوارزمية الترتيب بالإدراج، فيمكن إثبات أن الخوارزمية تعمل في زمن خطي متوقع ، حيث يُؤخذ المتوسط على جميع المدخلات الممكنة.^[3]

ومع ذلك، فإن أداء هذا النوع من الترتيب يتدهور عند حدوث تكتل (بالإنجليزية: clustering)، فعندما تقع قيم كثيرة متقاربة، فإنها ستتجمع في دلو واحد ويتم فرزها ببطء.

هذا التدهور في الأداء لا يحدث في خوارزمية فرز الدلاء الأصلية، لأنها تفترض أن المُدخلات (البيانات) موزعة توزيعًا عشوائيًا منتظمًا خلال الفترة [0،1).^[1]

على غرار الخوارزمية العامة للترتيب بالدلاء كما هو موضح أعلاه، تعمل خوارزمية الترتيب بخريطة التقارب (بالإنجليزية: ProxmapSort) عن طريق تقسيم مصفوفة المفاتيح إلى مصفوفات فرعية عبر استخدام دالة "مفتاح الخريطة" (بالإنجليزية: Map Key) التي تحافظ على ترتيب جزئي بين المفاتيح.

عندما يُضاف كل مفتاح إلى مصفوفته الفرعية، يتم استخدام خوارزمية الترتيب بالإدراج للحفاظ على ترتيب هذه المصفوفة الفرعية، مما يؤدي إلى أن تكون المصفوفة بأكملها مرتبة عند اكتمال تنفيذ الترتيب بخريطة التقارب.

تختلف خوارزمية الترتيب بخريطة التقارب عن خوارزميات الترتيب بطريقة الدلو من حيث أنها تستخدم "مفتاح الخريطة" لتحديد الموضع التقريبي للبيانات في الترتيب النهائي، فتُنتِ بذلك "خريطة التقارب" (بالإنجليزية: Proxmap) أي المواضع التقريبية التي ينبغي أن توضع فيها تلك المفاتيح مُرتبة.

هناك نوع آخر من خوارزمية الترتيب بالدلاء يُعرف باسم ترتيب المدرج التكراري (بالإنجليزية: Histogram sort) أو الترتيب بالعدّ (بالإنجليزية: Counting Sort)، يقوم بإضافة تمرير أوَّلي يعدّ فيه عدد العناصر التي ستقع في كل دلو، وذلك باستخدام مصفوفة عدّ (بالإنجليزية: Count Array).^[4]

وباستخدام هذه المعلومات، تُرتب قيم المصفوفة في سلسلة من الدلاء مباشرة داخل نفس المصفوفة عن طريق سلسلة من عمليات التبديل، مما يعني أنه لا توجد حاجة لمساحة إضافية لتخزين الدلاء.

ترتيب ساعي البريد (بالإنجليزية: Postman's sort) هو أحد أشكال خوارزمية الترتيب بطريقة الدلو، وهو يستفيد من البنية الهرمية للعناصر، والتي تُوصف عادةً بمجموعة من الخصائص.

هذه هي الخوارزمية التي تستخدمها آلات فرز الرسائل في مكاتب البريد:

1. حيث يُفرز البريد أولًا إلى محلي ودولي،
2. ثم حسب الولاية أو المقاطعة أو الإقليم،
3. ثم حسب مكتب البريد الوجهة،
4. ثم حسب خطوط التوزيع، وهكذا.

وبما أن المفاتيح لا تُقارن فيما بينها مباشرة، فإن الزمن اللازم للترتيب هو O( cn )، حيث تعتمد c على حجم المفتاح وعدد الدلاء.

وهذا يشبه إلى حد كبير الترتيب المنازلي (بالإنجليزية: Radix Sort) الذي يعمل "من الأعلى إلى الأسفل" أو ما يُعرف بترتيب "أكثر الأرقام أهمية أولًا" (بالإنجليزية: Most Significant Digit First).^[4]

الترتيب بالمجموعة التمهيدية أو الترتيب بالخلط (بالإنجليزية: Shuffle sort) هو أحد أشكال خوارزمية الترتيب بالدلاء والذي يبدأ بإزالة أول 1/8 من العناصر n المطلوب ترتيبها، ثم تُرتب هذه العناصر بشكل متكرر (بالإنجليزية: recursively) وتُوضَع في مصفوفة، وهذا يُنشئ عدد n /8 من الدلاء.^[5]

بعدها تُوزع الـ 7/8 من العناصر المتبقية على الدلاء السابقة التي تم إنشاءها من أول 1/8 من العناصر، ثم يُرتب كل "دلو" على حده.

وفي النهاية تُدمج جميع الدلاء في مصفوفة واحدة مُرتبة.

مكن اعتبار الترتيب بالدلو بمثابة تعميم للترتيب بالعد ؛ في الواقع، إذا كان حجم كل دلو 1، فإن ترتيب الدلو يتحول إلى ترتيب بالعدّ. يسمح حجم الدلو المتغير لترتيب الدلو باستخدام ذاكرة O( n ) بدلاً من ذاكرة O( M )، حيث M هو عدد القيم المميزة؛ في المقابل، فإنه يتخلى عن حساب أسوأ سلوك للترتيب O( n + M ).

يعتبر ترتيب الدلو باستخدام دلوين في الواقع نسخة من الترتيب السريع حيث يتم تحديد قيمة المحور دائمًا لتكون القيمة الوسطى لنطاق القيمة. في حين أن هذا الاختيار فعال بالنسبة للمدخلات الموزعة بشكل موحد، فإن الوسائل الأخرى لاختيار المحور في الترتيب السريع مثل المحاور المحددة عشوائيًا تجعله أكثر مقاومة للتجميع في توزيع المدخلات.

تبدأ خوارزمية الدمج ذات n طريقة أيضًا بتوزيع القائمة إلى n قائمة فرعية وترتيب كل واحدة منها؛ ومع ذلك، فإن القوائم الفرعية التي تم إنشاؤها بواسطة الدمج لها نطاقات قيمة متداخلة وبالتالي لا يمكن إعادة دمجها عن طريق التجميع البسيط كما هو الحال في الترتيب بطريقة الدلو. وبدلاً من ذلك، يجب أن يتم تداخلها بواسطة خوارزمية دمج. ومع ذلك، يتم موازنة هذه التكلفة الإضافية بمرحلة التشتت الأكثر بساطة والقدرة على ضمان أن يكون حجم كل قائمة فرعية هو نفسه، مما يوفر حدًا زمنيًا جيدًا في أسوأ الأحوال.

يمكن اعتبار الترتيب المنازلي من أعلى إلى أسفل بمثابة حالة خاصة من الترتيب بطريقة الدلو حيث يتم تقييد كل من نطاق القيم وعدد الدلاء ليكون قوة من اثنين. وبالتالي، فإن حجم كل دلو هو أيضًا قوة للرقم اثنين، ومن الممكن تطبيق الإجراء بشكل متكرر. يمكن أن يؤدي هذا النهج إلى تسريع مرحلة التشتت، حيث إننا نحتاج فقط إلى فحص بادئة التمثيل البت لكل عنصر لتحديد دلوه.

• بول إي. بلاك "ترتيب ساعي البريد" من قاموس الخوارزميات وهياكل البيانات في المعهد الوطني للمعايير والتكنولوجيا.
• روبرت رامي ، "صنف ساعي البريد" ، مجلة المستخدمين ، أغسطس 1992م.
• قاموس NIST للخوارزميات وهياكل البيانات: الترتيب بالدلاء

• رمز الترتيب بالدلاء لـ Ansi C.
• متغير الترتيب بالدلاء مع العرض التوضيحي نسخة محفوظة 14 أكتوبر 2014 على موقع واي باك مشين..