مسار دوبينز ا

في الهندسة الرياضية ، عادةً ما يشير مصطلح مسار دوبين إلى أقصر منحنى يربط بين نقطتين في المستوى الإقليدي الثنائي الأبعاد (أي المستوى xy ) مع وجود قيد على انحناء المسار ومع مماسات أولية ونهائية محددة للمسار، كما انه يفترض أن المركبة التي تسلك هذا المسار يمكنها التحرك للأمام فقط . أما إذا كانت المركبة قادرة على التحرك للخلف أيضًا، فإن المسار يتبع منحنى منحنى ريدز-شيب. ^[1] الذي يعد امتدادًا أو تعديلاً على مسار دوبنز ليأخذ في الحسبان إمكانية التحرك في الاتجاهين.

أثبت ليستر إيلي دوبينز (1920-2010) ^[2] باستخدام أدوات علم التحليل الرياضي ^[3] أن أي مسار من هذا النوع سيتألف من مقاطع ذات انحناء أقصى و/أو خطوط مستقيمة بمعنى آخر، سيتم إنشاء أقصر مسار من خلال ربط أقواس دائرية ذات أقصى انحناء وخطوط مستقيمة.

مناقشة

ي عام 1957، أثبت دوبنز نتائجه المتعلقة بمسارات دوبنز باستخدام أساليب التحليل الرياضي. بعد ذلك، في عام 1974، قدم هارولد هـ. جونسون إثباتًا آخر لنفس النتائج، من خلال تطبيق مبدأ بونترياجين الأقصى . ^[4] وضع هارولد جونسون شروطاً ضرورية وكافية لمنحنى مستوٍ، وهي ان يكون له انحناء متصل متسلسل محدد ونقاط واتجاهات أولية ونهائية محددة، لييصبح طولاً هو الأقصر بين جميع المسارات الممكنة. وفي عام 1992 تم إظهار نفس النتيجة مرة أخرى باستخدام مبدأ بونترياجين الأقصى. ^[5] في الآونة الأخيرة، تم تقديم دليل نظري لمنحنى هندسي بواسطة J. Ayala و D. Kirszenblat و J. Hyam Rubinstein. ^[6] وقد قدم J. Ayala دليلاً يميز مسارات دوبين في فئات التماثل. ^[7]

التطبيقات

يتم استخدام مسار دوبينز بشكل شائع في مجالات الروبوتات ونظرية التحكم كطريقة لتخطيط المسارات للروبوتات ذات العجلات والطائرات والمركبات تحت الماء. توجد طرق هندسية بسيطة ^[8] وطرق تحليلية ^[9] لحساب المسار الأمثل.

على سبيل المثال، في حالة الروبوت ذي العجلات، يكون نموذج السيارة الحركية البسيطة (المعروفة أيضًا باسم سيارة دوبينز) للأنظمة هو: ${\begin{aligned}{\dot {x}}&=V\cos(\theta )\\{\dot {y}}&=V\sin(\theta )\\{\dot {\theta }}&=u\end{aligned}}$ بحيث $(x,y)$ هو موقع السيارة، $\theta$ هو اتجاه السيارة ، كما ان $V$ هي السرعة الثابتة التي تتحرك بها السيارة و u معدل التحكم في الالتفاف، وهو محدود بقيمة قصوى. في هذه الحالة، يصبح معدل الدوران الأقصى مساوي للحد الأدنى لنصف قطر الدوران (وبالمثل الحد الأقصى للانحناء). كما ان المماسات الأولية والنهائية الموصوفة تطابق مع العناوين الأولية والنهائية. يعطي مسار دوبينز أقصر مسار يربط بين نقطتين موجهتين وهو ما يمكن تنفيذه في نموذج الروبوت ذي العجلات.

يمكن وصف نوع المسار الأمثل باستخدام تشبيه بالسيارات من خلال القيام "بالانعطاف إلى اليمين (R)"، أو "الانعطاف إلى اليسار (L)"، أو القيادة "بشكل مستقيم (S)." سيكون المسار الأمثل دائمًا واحدًا على الأقل من الأنواع الستة: RSR، وRSL، وLSR، وLSL، وRLR، وLRL. على سبيل المثال، لنفترض أنه بالنسبة لبعض المواضع الأولية والنهائية والمماسات المعطاة، يتبين أن المسار الأمثل هو من نوع "RSR". وهذا يتوافق مع قوس انعطاف يمين (R) يتبعه قطعة مستقيمة (S) يتبعها قوس انعطاف يمين آخر (R). التحرك على طول كل جزء في هذا التسلسل للحصول على الطول المناسب سيشكل أقصر منحنى يربط نقطة البداية A بنقطة النهاية B مع المماسات المطلوبة في كل نقطة نهاية والتي لا تتجاوز الانحناء المعطى.

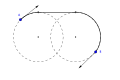
مسار RSL Dubins
مسار RSR Dubins
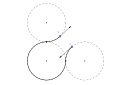
مسار LRL Dubins

مسألة فاصلة دوبين

تعتبر مسألة الفترات لمسار دوبنز نوعًا متقدمًا من مسألة مسار دوبنز الأساسية، حيث يتم تحديد مجال (فترة) من الاتجاهات الممكنة عند نقطتي البداية والنهاية بدلاً من تحديد اتجاه محدد بدقة. في هذه الحالة يتم تقييد الاتجاه المماس للمسار عند النقاط الأولية والنهائية بحيث يقع ضمن الفواصل الزمنية المحددة. يمكن حل هذه المشكلة باستخدام التحليل الهندسي، ^[10] أو باستخدام مبدأ الحد الأدنى لبونترياجين. ^[11]

مراجع

^ Reeds، J. A.؛ Shepp، L. A. (1990). "Optimal paths for a car that goes both forwards and backwards". Pacific Journal of Mathematics. ج. 145 ع. 2: 367–393. DOI:10.2140/pjm.1990.145.367.
^ "IN MEMORIAM Lester Eli Dubins Professor of Mathematics and Statistics, Emeritus UC Berkeley 1920–2010". University of California. مؤرشف من الأصل في 2011-09-15. اطلع عليه بتاريخ 2012-05-26.
^ Dubins، L. E. (يوليو 1957). "On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents". American Journal of Mathematics. ج. 79 ع. 3: 497–516. DOI:10.2307/2372560. JSTOR:2372560.
^ Johnson، Harold H. (1974). "An application of the maximum principle to the geometry of plane curves". Proceedings of the American Mathematical Society. ج. 44 ع. 2: 432–435. DOI:10.1090/S0002-9939-1974-0348631-6. MR:0348631.
^ Boissonat، J.-D.؛ Cerezo، A.؛ Leblond، K. (مايو 1992). Shortest Paths of Bounded Curvature in the Plane (PDF). Piscataway, NJ. ج. 3. ص. 2315–2320. DOI:10.1109/ROBOT.1992.220117. مؤرشف من الأصل (PDF) في 2012-05-03.
^ Ayala، José؛ Kirszenblat، David؛ Rubinstein، Hyam (2018). "A Geometric approach to shortest bounded curvature paths". Communications in Analysis and Geometry. ج. 26 ع. 4: 679–697. arXiv:1403.4899. DOI:10.4310/CAG.2018.v26.n4.a1.
^ Ayala، José (2015). "Length minimising bounded curvature paths in homotopy classes". Topology and Its Applications. ج. 193: 140–151. arXiv:1403.4930. DOI:10.1016/j.topol.2015.06.008.
^ Anisi، David (يوليو 2003). Optimal Motion Control of a Ground Vehicle (PDF) (Report). Swedish Research Defence Agency. 1650-1942. مؤرشف من الأصل (PDF) في 2024-05-03.
^ Bui، Xuan-Nam؛ Boissonnat، J.-D.؛ Soueres، P.؛ Laumond، J.-P. (مايو 1994). Shortest Path Synthesis for Dubins Non-Holonomic Robot. San Diego, CA. ج. 1. ص. 2–7. DOI:10.1109/ROBOT.1994.351019.
^ Manyam، Satyanarayana؛ Rathinam، Sivakumar (2016). "On Tightly Bounding the Dubins Traveling Salesman's Optimum". Journal of Dynamic Systems, Measurement, and Control. ج. 140 ع. 7: 071013. arXiv:1506.08752. DOI:10.1115/1.4039099. S2CID:16191780.
^ Manyam، Satyanarayana G.؛ Rathinam، Sivakumar؛ Casbeer، David؛ Garcia، Eloy (2017). "Tightly Bounding the Shortest Dubins Paths Through a Sequence of Points". Journal of Intelligent & Robotic Systems. ج. 88 ع. 2–4: 495–511. DOI:10.1007/s10846-016-0459-4. S2CID:30943273.

روابط خارجية

منحنيات دوبينز نسخة محفوظة 2016-03-22 على موقع واي باك مشين. من كتاب خوارزميات التخطيط لستيفن م. لافالي
خطوط التوقيت لسيارة دوبينز ، عرض توضيحي من مشروع العروض التوضيحية لشركة ولفرام
تنفيذ مفتوح المصدر لـ Python Reeds-Shepp ، من تأليف Built Robotics

[1] Reeds، J. A.؛ Shepp، L. A. (1990). "Optimal paths for a car that goes both forwards and backwards". Pacific Journal of Mathematics. ج. 145 ع. 2: 367–393. DOI:10.2140/pjm.1990.145.367.

[2] "IN MEMORIAM Lester Eli Dubins Professor of Mathematics and Statistics, Emeritus UC Berkeley 1920–2010". University of California. مؤرشف من الأصل في 2011-09-15. اطلع عليه بتاريخ 2012-05-26.

[3] Dubins، L. E. (يوليو 1957). "On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents". American Journal of Mathematics. ج. 79 ع. 3: 497–516. DOI:10.2307/2372560. JSTOR:2372560.

[4] Johnson، Harold H. (1974). "An application of the maximum principle to the geometry of plane curves". Proceedings of the American Mathematical Society. ج. 44 ع. 2: 432–435. DOI:10.1090/S0002-9939-1974-0348631-6. MR:0348631.

[5] Boissonat، J.-D.؛ Cerezo، A.؛ Leblond، K. (مايو 1992). Shortest Paths of Bounded Curvature in the Plane (PDF). Piscataway, NJ. ج. 3. ص. 2315–2320. DOI:10.1109/ROBOT.1992.220117. مؤرشف من الأصل (PDF) في 2012-05-03.

[6] Ayala، José؛ Kirszenblat، David؛ Rubinstein، Hyam (2018). "A Geometric approach to shortest bounded curvature paths". Communications in Analysis and Geometry. ج. 26 ع. 4: 679–697. arXiv:1403.4899. DOI:10.4310/CAG.2018.v26.n4.a1.

[7] Ayala، José (2015). "Length minimising bounded curvature paths in homotopy classes". Topology and Its Applications. ج. 193: 140–151. arXiv:1403.4930. DOI:10.1016/j.topol.2015.06.008.

[8] Anisi، David (يوليو 2003). Optimal Motion Control of a Ground Vehicle (PDF) (Report). Swedish Research Defence Agency. 1650-1942. مؤرشف من الأصل (PDF) في 2024-05-03.

[9] Bui، Xuan-Nam؛ Boissonnat، J.-D.؛ Soueres، P.؛ Laumond، J.-P. (مايو 1994). Shortest Path Synthesis for Dubins Non-Holonomic Robot. San Diego, CA. ج. 1. ص. 2–7. DOI:10.1109/ROBOT.1994.351019.

[10] Manyam، Satyanarayana؛ Rathinam، Sivakumar (2016). "On Tightly Bounding the Dubins Traveling Salesman's Optimum". Journal of Dynamic Systems, Measurement, and Control. ج. 140 ع. 7: 071013. arXiv:1506.08752. DOI:10.1115/1.4039099. S2CID:16191780.

[11] Manyam، Satyanarayana G.؛ Rathinam، Sivakumar؛ Casbeer، David؛ Garcia، Eloy (2017). "Tightly Bounding the Shortest Dubins Paths Through a Sequence of Points". Journal of Intelligent & Robotic Systems. ج. 88 ع. 2–4: 495–511. DOI:10.1007/s10846-016-0459-4. S2CID:30943273.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]