شبه منحرف
شبه منحرف
النوع	رباعي أضلاع
الحواف والرأس	4
المساحة	${\displaystyle {\tfrac {a+b}{2}}h}$
الخصائص	محدب

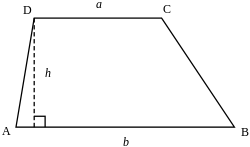
شبه المنحرف^[1] هو رباعي أضلاع فيه ضلعان متقابلان متوازيان. ويراعى أنه يتم استثناء متوازي الأضلاع من هذا التعريف الذي غالباً ما يعتبر حالة خاصة من شبه المنحرف. كان يطلق عليه اسم ذو الزنقة في عصر الحضارة الإسلامية.^[2]

لتكن K مساحة شبه منحرف كيفي

K بدلالة القاعدتين الكبرى والصغرى والارتفاع تكون: ${\displaystyle K={\frac {a+b}{2}}\cdot h}$

K بدلالة الأضلاع الأربعة تكون:${\displaystyle K={\frac {a+b}{|b-a|}}{\sqrt {(s-b)(s-a)(s-b-c)(s-b-d)}}}$

حيث أن: ${\displaystyle s={\tfrac {1}{2}}(a+b+c+d)}$

K حسب علاقة بريتشنايدر:${\displaystyle K={\sqrt {{\frac {(ab^{2}-a^{2}b-ad^{2}+bc^{2})(ab^{2}-a^{2}b-ac^{2}+bd^{2})}{(2(b-a))^{2}}}-\left({\frac {b^{2}+d^{2}-a^{2}-c^{2}}{4}}\right)^{2}}}}$

جزء من سلسلة مقالات حول
رباعيات الاضلاع
أنواع
متوازي أضلاع (متقاطع)  · مُعيّن  · مستطيل  · مربع  · شبه منحرف (متساوي الساقين  · مماسي)  · طائرة ورقية (قائمة الزاويتان)  · رباعي أضلاع مقعر
تصنيف
متساوي الأقطار  · متعامد الأقطار [الإنجليزية]‏  · دائري (ثنائي المركز) · مماسي (مماسي خارجي)  · لامبرت  · ساتشري
مواضيع ذات صلة
هندسة إقليدية  · مضلع  · ضلع  · زاوية  · مثلث  · دائرة
بوابة هندسة رياضية
ع ن ت

ارتفاع شبه المنحرف بدلالة الأضلاع الأربعة يكون حسب العلاقة التالية:

${\displaystyle h={\frac {\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}{2|b-a|}}}$

القاعدتان الكبرى والصغرى لشبه منحرف كيفي بدلالة القطرين والضلعين الجانبيين حسب علاقة بن عيشة جمال الدين:

${\displaystyle b={\sqrt {\frac {(c^{2}-p^{2})^{2}-(d^{2}-q^{2})^{2}}{2(c^{2}+p^{2})-2(d^{2}+q^{2})}}}}$

${\displaystyle a={\sqrt {\frac {(d^{2}-p^{2})^{2}-(c^{2}-q^{2})^{2}}{2(d^{2}+p^{2})-2(c^{2}+q^{2})}}}}$

حيث أن AC=p، BD=q، AD=c و BC=d مع p لايساوي q.

يمكن استعمال علاقة جمال في اثبات توازي مستقيمين، حيث بالنسبة للشكل الذي لدينا: إذا كان 0<b² فإن a و b متوازيان، وإذا كان b²<0 فإن a و b غير متوازيين.

يمكن حساب قطري شبه المنحرف انطلاقا من الأطوال الأربعة باستخدام العلاقة التالية:

${\displaystyle p={\sqrt {\frac {ab^{2}-a^{2}b-ac^{2}+bd^{2}}{b-a}}}}$

${\displaystyle q={\sqrt {\frac {ab^{2}-a^{2}b-ad^{2}+bc^{2}}{b-a}}}}$

مع p لايساوي q. الا في حالة ان يكون شبه المنحرف متطابق الساقين

• شبه منحرف متساوي الساقين
• متوازي الأضلاع

• Weisstein, Eric W. "شبه منحرف". MathWorld.

هذه بذرة مقالة عن الهندسة الرياضية بحاجة للتوسيع. فضلًا شارك في تحريرها.